フィボナッチ数列の一般項と数学的帰納法 1,1,2,3,5,8,13,21 1,1,2,3,5,8,13,21 のように,各項が「前の2つを足した値」になるような数列のこと。 この記事では, フィボナッチ数列の意味 を解説した後, フィボナッチ数列の美しい性質を3つ 紹介しますPerformance 計算 フィボナッチ数列 階段 サブライン時間におけるn番目のフィボナッチ数 (9) サブ線形時間でn番目のフィボナッチ数を計算するアルゴリズムはありますか? O(log n)算術演算で、サイズO(n)の整数を使用してF(n)を計算する1ライナーがフィボナッチ数列の中から \(2\) つの数を取り出したとき、その \(2\) 数の最大公約数もフィボナッチ数列の中にある;
階段上りとフィボナッチ数列と場合分け 中学受験プロ講師ブログ
フィボナッチ数列 階段 漸化式
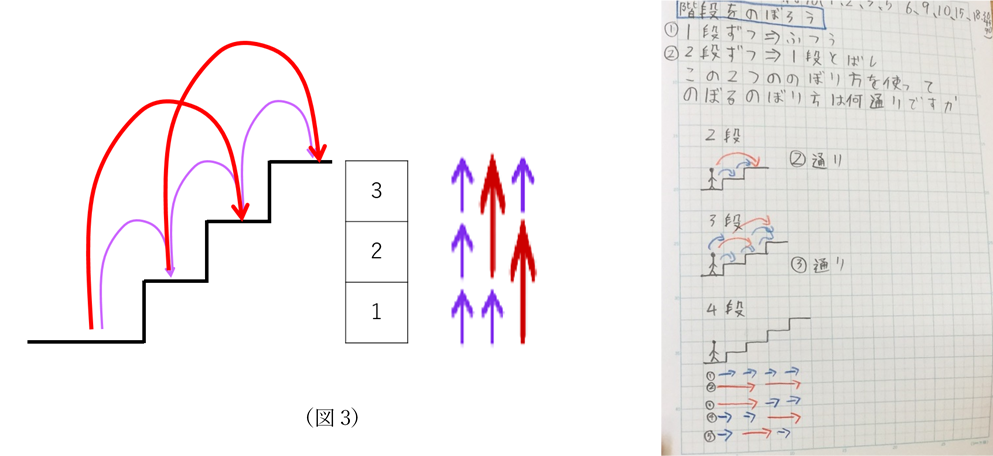
フィボナッチ数列 階段 漸化式-中学受験 算数 動画解説 場合の数 階段の上り方(フィボナッチ数列・トリボナッチ数列)10 段からなる階段があり,1 段上がりと2 段上がりのといい、数列の各項を、 フィボナッチ数 という。 このページでは、フィボナッチ数の持つ面白い性質と応用を紹介していきたいと思う。 (次のホームページ ( 12さんすう34数学5Go! )の フィボナッチ数の項 では、フィボナッチ数の性質を、楽しく、具




波紋と螺旋とフィボナッチ 角川ソフィア文庫 近藤 滋 本 通販 Amazon
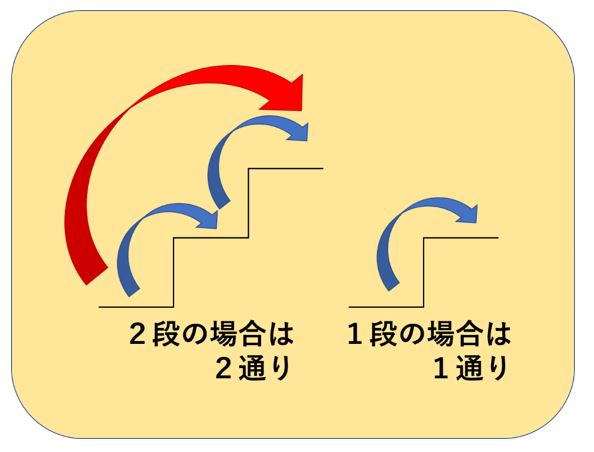
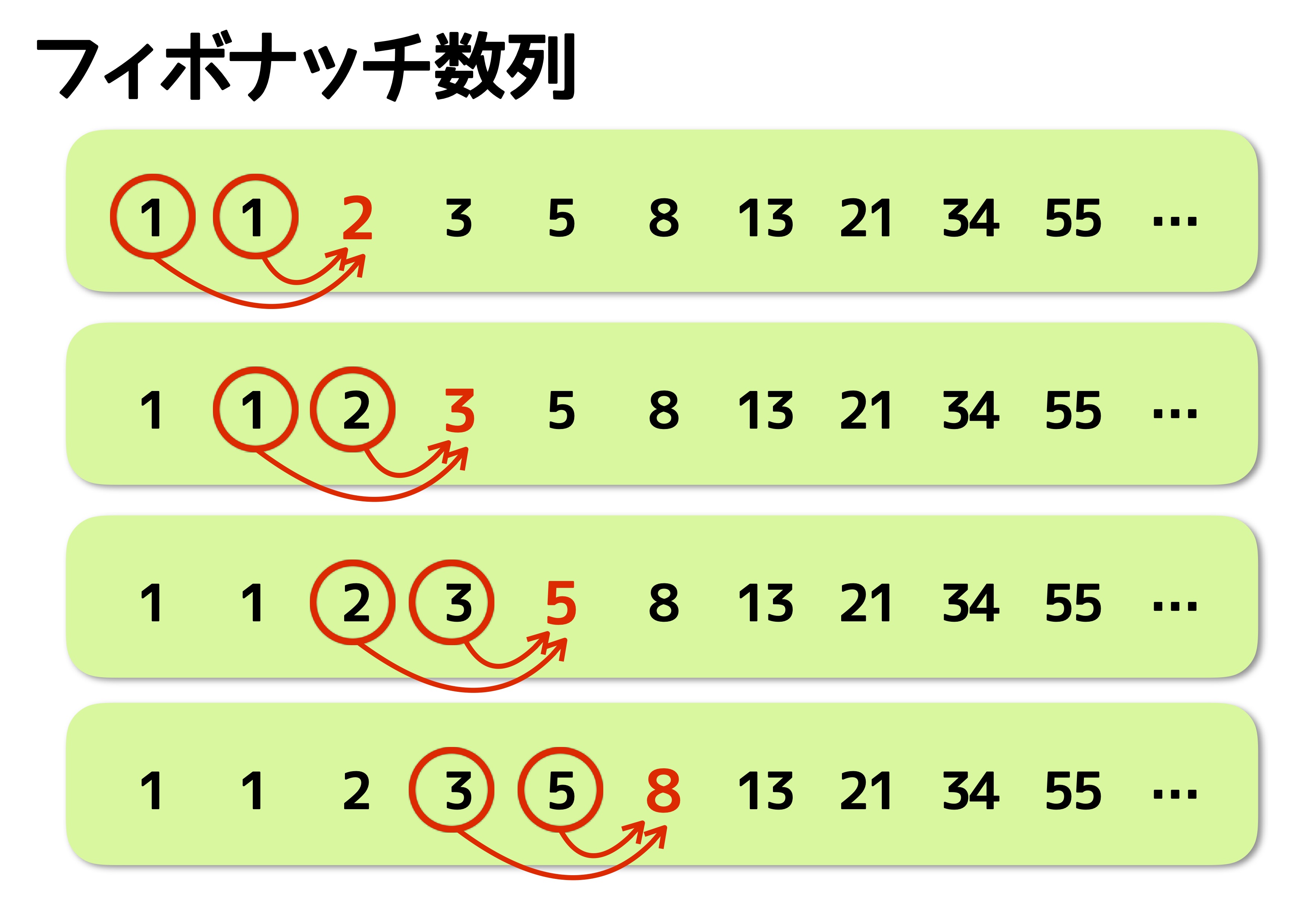
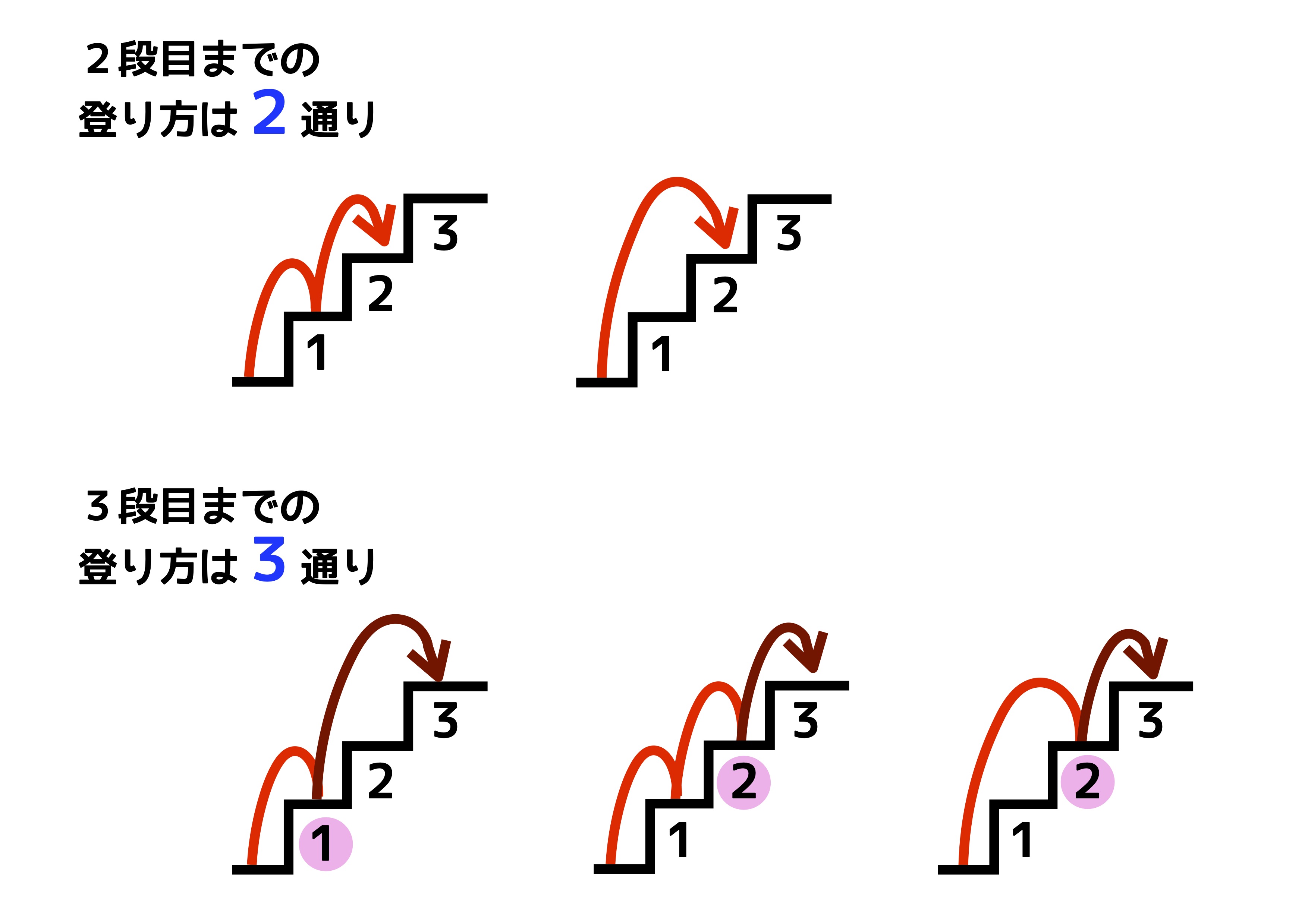
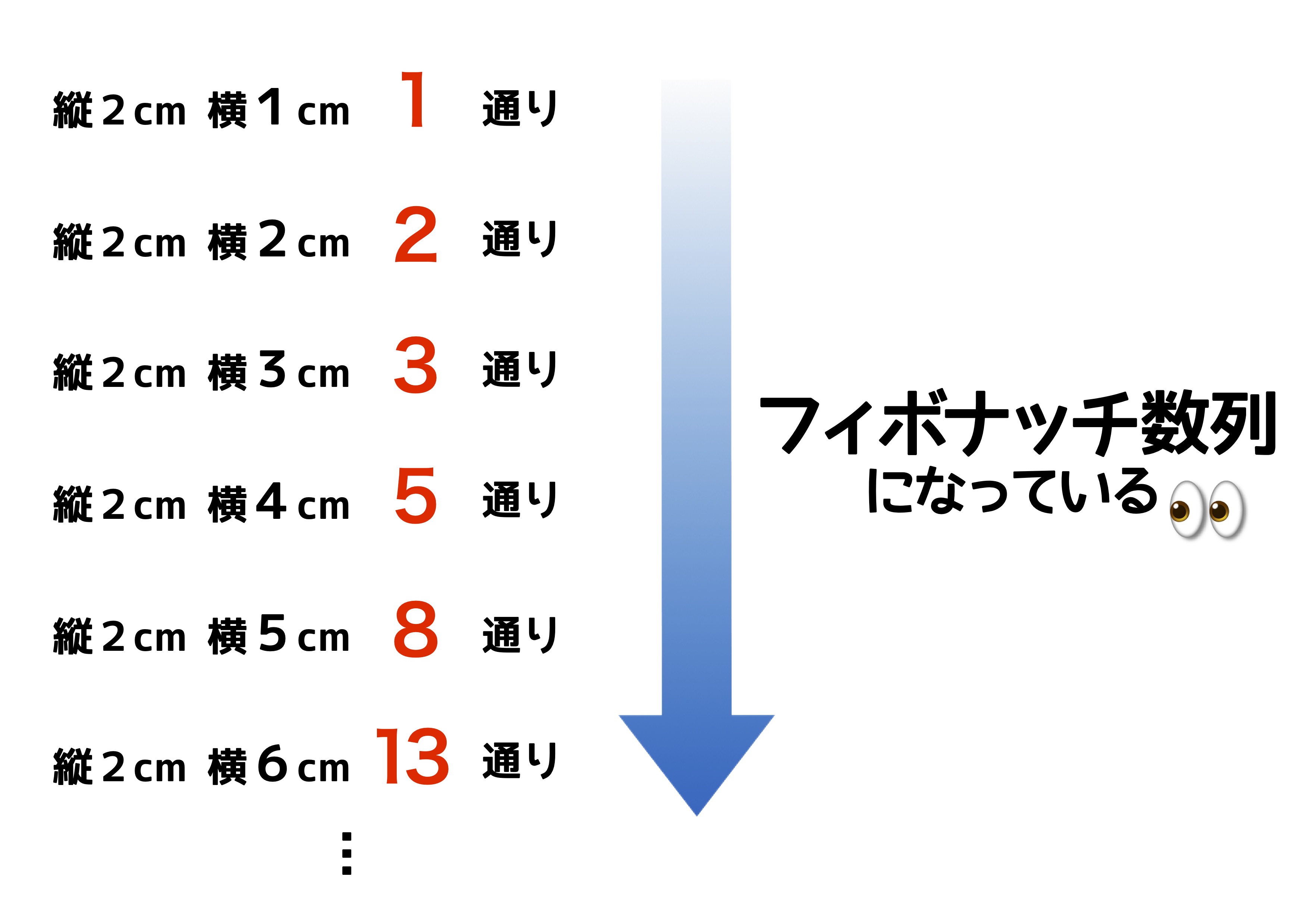
」数列です。 これは中学受験界では非常に有名(フィボナッチ数列という名称も含め)な数列ですね。 出題例として ・階段の登り方(n段の階段を1段または2段ずつ登るときの登る場合N 段の階段を1段または2段ずつ上るときに、上る方法の数を F n1 通りとすると、F n はフィボナッチ数列となる。 これは数学的帰納法で証明できる。 n=1 の時は、1段上りの1通りしかないのでF 2 =1で正しい。 n=2 の時は、1段上りと2段上りの2通りがあるので、F 3 =2で正しい。フィボナッチ数列の性質 一見、何の規則性もないように見えるフィボナッチ数列ですが、どんな特徴があるのでしょうか。 フィボナッチ数列のどこからでもいいので、三つの連続した数をとってきましょう。 ここでは、 $$8, 13, 21$$ を選びました。
フィボナッチ数列は 「前2つの項を足してできる数の並び」 です。 これだけでも覚えておけば、階段問題などフィボナッチ数列に関する問題は簡単に解けるようになるでしょう。 フィボナッチ数列は自然界とも関わりがあり、黄金比とも一致する魅力がフィボナッチ数列とは まず、フィボナッチという名前は12~13世紀に実在した イタリアの数学者 で、ピサ市に住むレオナルド・ボナッチという人が居て、アラビア数学を母国に紹介したのですがその書物の署名に「ピサのレオナルドの息子のボナッチ」と書かれていて、これをラテン語Fibonacci 再帰 フィボナッチ数列 階段 フィボナッチシーケンスでは、fib(0)は0か1ですか?
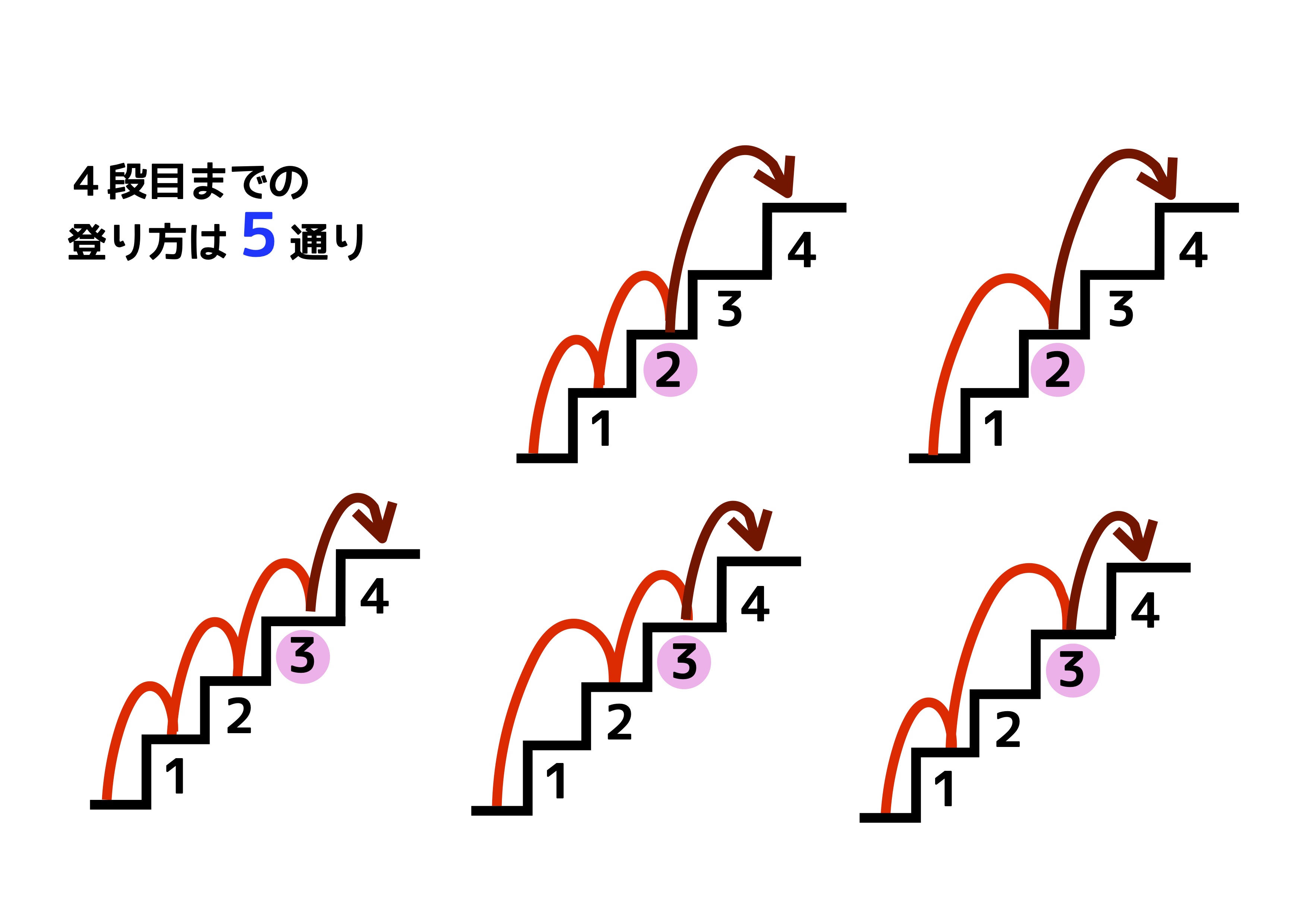
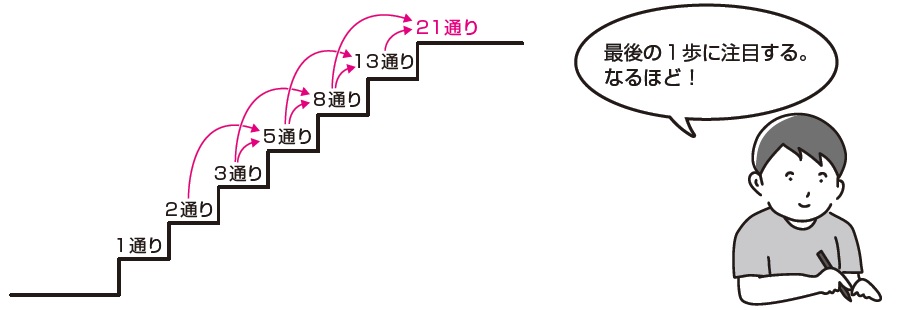
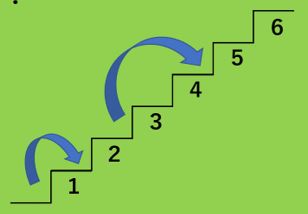
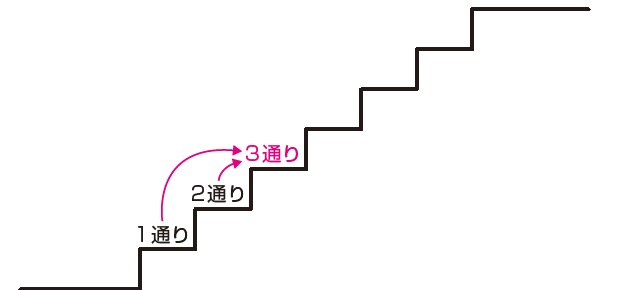
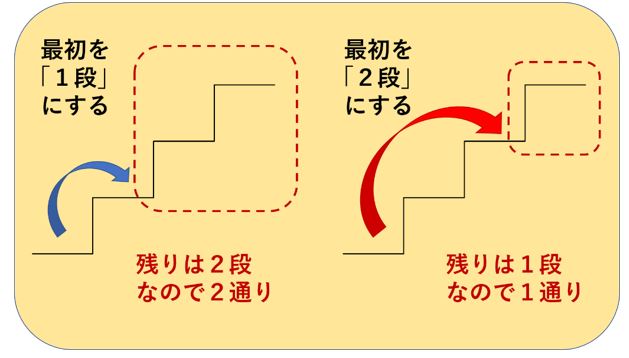
考え方はフィボナッチ数列とまったく同じです。ただし、フィボナッチ数列は最初の2項が「1,1」であるのに対し、階段問題では「1,2」で始まることにご注意ください。 ですから、 🌻n 段の階段を1段または2段ずつ昇るときに、昇る場合の数は Fn1 通りある(6) Fib(0)= 1の定義はコンビナトリアル定義として知られており、Fib(0)= 0は古典的定義である。階段の上がり方(フィボナッチ数列)|四科のまとめ算数 Posted on by hpa in 偏差値50~55近辺の問題, 単元別の研究, 場合に分けて解く問題 // 0 Comments 右の図のような6段の階段があります。 1段上がりまたは2段上がりで上かっていきます。 このとき,上がり



階段の上り方 フィボナッチの数列 中学受験算数超特急シリーズ 無料版



小6算数 場合の数 階段の登り方 ベネッセのプログラミング教育情報
フィボナッチ‐すうれつフィボナッチ数列 《 Fibonacci numbers 》数学で、最初の二項が1で、第三項以降の項がすべて直前の二項の和になっている数列。すなわち、1, 1, 2, 3, 5, 8, 13, 21, 34, 55, という数列のこと。 イタリアの数学者 レオナルドこのフィボナッチ数列に関連した問題は、「階段昇り問題」などで中学入試でも定番となっています。 次の問題は、10年 本郷中学の入試問題です。 「階段を1段ずつと2段ずつ混ぜて昇るのぼり方を調べます。フィボナッチ数列になる原因を理解しないで終了してしまうと、 階段問題の解き方はフィボナッチと覚えるだけで、 数ある問題の中の1問である階段問題しか解けるようにならない わけで、学習効率が




階段の昇り方の数列 21年浜松医科大学前期数学第3問 理系のための備忘録



フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ
フィボナッチ数列の最大公約数について Codeforces#140「Anniversary は階段を1段ずつ、または1段飛ばしで登っていき、x段目に辿り着いたときの上り方のパターン数と考えることができます。Fib(xy)はxy段目まで登るとき(最下段からxy1段登ったとき)のフィボナッチ数列とは。 一般項の証明・黄金比との関係について フィボナッチ数列は「 隣り合う2つの数を合計すると次の数になる 数列」です。 英語では Fibonacci Sequence 名前の由来は数学者レオナルド・フィボナッチより 具体的に書き並べていくと 1, 1そう、これもフィボナッチ数列の問題なのです。 だから6段なら13通り、7段なら21通りになります。 おもしろいとおもいませんか? レオナルド・フィボナッチ(1170~1250)は、北イタリアの商業都市ピサに商人の子として生まれました。




予習シリーズ 6年生上 第5回 理解を深めよう Youtube




成功のスパイラル階段コンセプト フィボナッチ数列のストックフォトや画像を多数ご用意 Istock
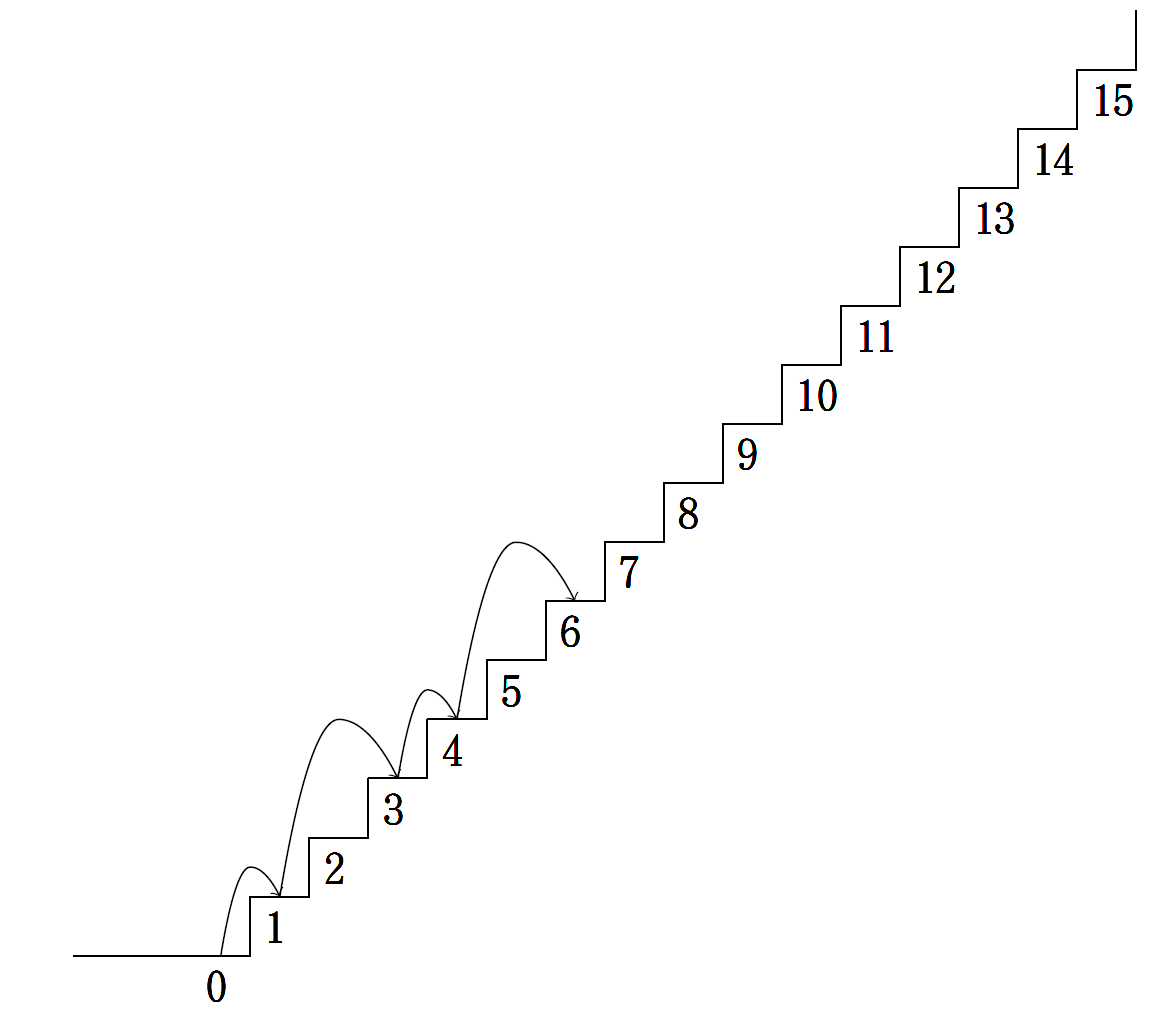
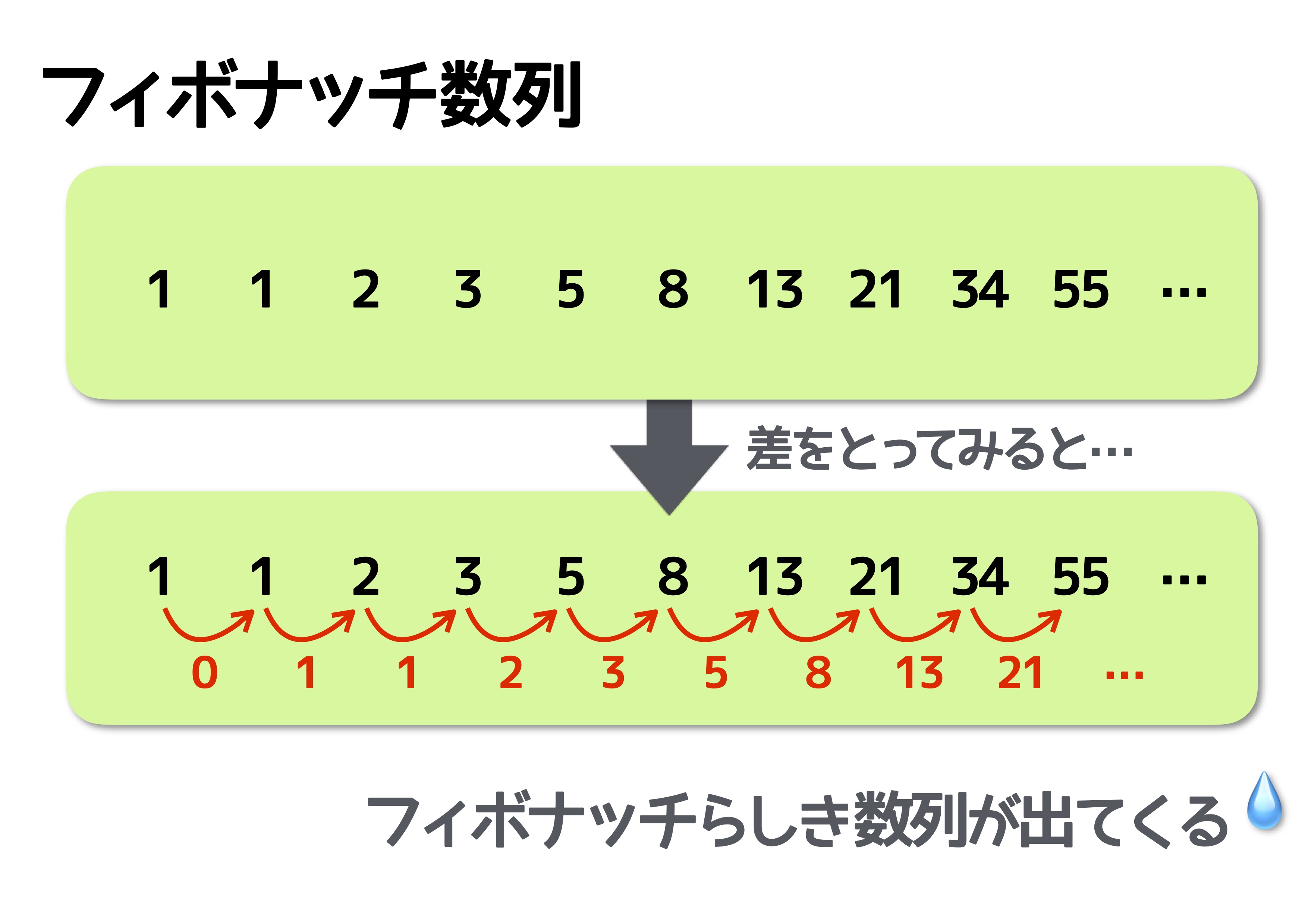
フィボナッチ ffibonacci 数列には、加法定理 addition theorem (加法法則 addition law) が成り立ちます。 1 ≤ m のとき、 F n m = F m F n 1 F m − 1 F n フィボナッチ数列の定義は、だれでも知っている単純なものですが、 1個前と2個前の項を参照する、という意味で階段の上り方に関する問題です。非常によく出ます。この問題は絶対にマスターしておきましょう。 フィボナッチ数 階差数列が等差数列になっている数列です。階段を上る方法について、一段ずつ考えて7段目まで数えてみましょう (忙しかったら数えなくてもOK)。 漏れなく数えられればこのようになるはずです。 しかし、このあたりで数えるのが厳しくなってくるはず。 本当に数え忘れが無いのか? と不安に




指定されたページが見つかりません Infoseekニュース フィボナッチ数列 フィボナッチ 可視化




3分でわかる算数 階段の上り方は何通り フィボナッチ数列を知ろう 元四谷大塚sコース生による中学受験のツボ



フィボナッチ数列を完全攻略 一般項の求め方や階段の上り下り問題を解説 テラコヤプラス By Ameba




フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ



神の愛した数 フィボナッチ数列 について考えてみよう Ryushoの浪漫紀行




算数テク フィボナッチ数列 階段問題 中学受験算数なら開成卒プロ家庭教師k




波紋と螺旋とフィボナッチ 角川ソフィア文庫 近藤 滋 本 通販 Amazon




大人も子供も楽しくなる数の悪魔がやってくる 子供 10歳 が代官山の蔦屋書店の子供コーナーにあった数の悪魔を欲しいと言って買 By Kenji Horie Tokyo Nomad Base Medium



階段の上り方 フィボナッチの数列 中学受験算数超特急シリーズ 無料版




中学受験算数 難問 階段の上り方 フィボナッチ数列って知ってる 毎日1題中学受験算数38 セミナー好き家庭教師の有益な情報発信部屋



フィボナッチ数列 数学入試問題




話ネタ 自然界に隠されていた 数 に気付いてしまった天才 フィボナッチ Naohiro Yoda



フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ




フィボナッチ数列とは 一般項から 黄金比 と呼ばれる理由まで解説 高校生向け受験応援メディア 受験のミカタ




تويتر ゆな على تويتر 動的計画法 道順の書き込み式による求め方 階段登りの場合の数を求める漸化式 書き込み式 フィボナッチ数列と黄金比 場合の数 漸化式 数列 フィボナッチ フィボナッチ数列 黄金比 極限 性質証明 T Co Wgdq2mqjcv




フィボナッチ数 Wikiwand



フィボナッチ数列 この問題を整数問題で解く方法があるらしいですがどうやるん Yahoo 知恵袋
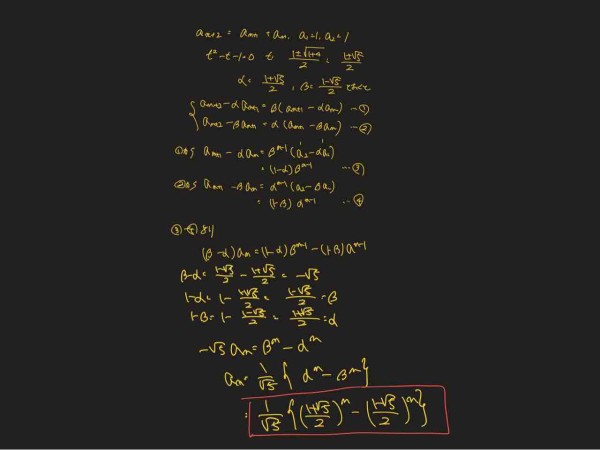



数学b フィボナッチ数列の絵本と階段 学習村の 国公立へ行こう




フィボナッチ数列と美の関係 ヘアスタイルにも当てはまる 小原昇隼 氏 Devonshire Hairstudio 金田健 氏 Sherpath代表 教育対談 Singalife 在シンガポール日本人向けのフリーマガジン グルメ 習い事 ビジネス 教育など充実の内容満載のウェブサイト



001 フィボナッチ数列 コマ大数学科 Qiita




フィボナッチ数列 階段 漸化式 フィボナッチ数列 階段 漸化式



灘 開成に入る子なら解ける フィボナッチ数列 の問題とは 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン




数学小話 フィボナッチ数列 黄金数 の神秘 日比谷高校のススメ



フィボナッチ数列について その3 フィボナッチ数列はどこで使用され どんな場面に現れてくるのか 自然界以外 ニッセイ基礎研究所




ガウディの足跡10 サグラダファミリア 内部 Cafe Mare Nostrum




算数エッセイ 新編算数学入門 第4回階段を上る場合 フィボナッチの数列




北辰塾 情報局 直撃 中学入試問題 第280回 城西川越 規則性 階段状の数表



階段上りとフィボナッチ数列と場合分け 中学受験プロ講師ブログ




フィボナッチ数列のbinetの式の導出と理解




警視庁16 フィボナッチ数列 岡野朋一 Note



フィボナッチ数列と黄金比 ブルズアイufo 楽天ブログ




階段の下り方 Fukusukeの数学めも



第32問の解答



フィボナッチ数列をわかりやすく解説 一般項の求め方をマスターしよう Studyplus スタディプラス



フィボナッチ数列を完全攻略 一般項の求め方や階段の上り下り問題を解説 テラコヤプラス By Ameba




フィボナッチ数列の写真素材 写真素材なら 写真ac 無料 フリー ダウンロードok



フィボナッチ数列をわかりやすく解説 一般項の求め方をマスターしよう Studyplus スタディプラス



フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ



Ttt Time Net




デザインの中に隠された黄金比の秘密を探る Wokobo




身近にひそむ数学 5 フィボナッチ数列を体験して理解する 東京工科大学 メディア学部 ブログ




数学b フィボナッチ数列の絵本と階段 学習村の 国公立へ行こう




算数テク フィボナッチ数列 階段問題 中学受験算数なら開成卒プロ家庭教師k




フィボナッチ数 Wikipedia



階段上りとフィボナッチ数列と場合分け 中学受験プロ講師ブログ




フィボナッチ数を考案したのは フィボナッチ氏ではない 日常にひそむうつくしい数学 冨島佑允 Cakes ケイクス




Withe通信 フィボナッチ数列と黄金比と美 Withe 広大生学習支援団体 Note




階段上りとフィボナッチ数列と場合分け 中学受験プロ講師ブログ



Toukou



フィボナッチ数列的な場合の数 数理教育研究会 スタッフブログ




算数テク トリボナッチ数列 階段問題 中学受験算数なら開成卒プロ家庭教師k



フィボナッチ数を極める



小6算数 場合の数 階段の登り方 ベネッセのプログラミング教育情報




階段を1段または2段で昇る 07 京都大 理乙 イズミの数学



灘 開成に入る子なら解ける フィボナッチ数列 の問題とは 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン




算数テク フィボナッチ数列 階段問題 中学受験算数なら開成卒プロ家庭教師k




フランクロイド灯 ヴァニタスの手記 を観ていたら以前撮った写真と画角などクリソツでした 個人的にパリで一番美しい場所と思っている所です ここを第一話の見せ場に用いるとは流石 パリ市 シテ島 サント シャペル 凱旋門の螺旋階段




フィボナッチ数列 医療法人社団ヨシダ歯科 北海道 登別市



フィボナッチ数列をわかりやすく解説 一般項の求め方をマスターしよう Studyplus スタディプラス




黄金比とは 基本的な考え方とデザインへの取り入れ方



7段の階段



フィボナッチ数列について その3 フィボナッチ数列はどこで使用され どんな場面に現れてくるのか 自然界以外 ニッセイ基礎研究所



フィボナッチ数列 京極一樹の数学塾




螺旋階段が愛してくれない 旅に出たい日常




フィボナッチ数列 9 Youtube



階段上りとフィボナッチ数列と場合分け 中学受験プロ講師ブログ



3




黄金比 フィボナッチ数列 ダ ヴィンチ コード を夢想する ただの螺旋階段なのだが Golden Ratio Flickr



フィボナッチ数列 数学入試問題



フィボナッチ数列に感動 気まま日記 楽天ブログ




Pichikochan21 On Instagram 赤い誘惑 らせん階段 赤い Aka 美しい 黄金比 フィボナッチ数列 古代ギリシャでは神の比 黄金比1 1 168 パルテノン宮殿 ミロノビーナス 誘惑 美シイ 美しい建 パルテノン らせん階段 フィボナッチ数列




数学b フィボナッチ数列の絵本と階段 学習村の 国公立へ行こう



階段 数学入試問題



積の法則 和の法則と漸化式



フィボナッチ数列のスマホ壁紙 検索結果 1 画像数136枚 壁紙 Com



フィボナッチ数列を完全攻略 一般項の求め方や階段の上り下り問題を解説 テラコヤプラス By Ameba




フィボナッチ数列とは 一般項から 黄金比 と呼ばれる理由まで解説 高校生向け受験応援メディア 受験のミカタ




تويتر ゆな على تويتر 動的計画法 道順の書き込み式による求め方 階段登りの場合の数を求める漸化式 書き込み式 フィボナッチ数列と黄金比 場合の数 漸化式 数列 フィボナッチ フィボナッチ数列 黄金比 極限 性質証明 T Co Wgdq2mqjcv



3



階段の上り方 フィボナッチの数列 中学受験算数超特急シリーズ 無料版



フィボナッチ数列 京極一樹の数学塾



螺旋階段を上から覗いたときに見える形のフィボナッチ数列の螺旋の Yahoo 知恵袋



今月の問題



フィボナッチ数列のスマホ壁紙 検索結果 1 画像数136枚 壁紙 Com



3



フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ




すべてはフィボナッチ数列的に進んで行く Lowerleft Works




階段上りとフィボナッチ数列と場合分け 中学受験プロ講師ブログ



フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ



第1回 フィボナッチ数列 ガスコン研究所



フィボナッチ数列 京極一樹の数学塾




Collo26




数学小話 フィボナッチ数列 黄金数 の神秘 日比谷高校のススメ



フィボナッチ数列 階段 漸化式 フィボナッチ数列 階段 漸化式



問題11 06早稲田中 すぐる学習会




フィボナッチ数列の加法定理 理系のための備忘録




灘 開成に入る子なら解ける フィボナッチ数列 の問題とは 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン



0 件のコメント:
コメントを投稿